Due to change in the temperature, the material expands or contract. The amount δT is given by
δT=αL(Tf−Ti)=αLΔT
where α is the coefficient of thermal expansion in m/m°C, L is the length in meter, Ti and Tf are the initial and final temperatures, respectively in °C. For steel, α= 11.25 × 10-6 m/m°C.
If temperature deformation is permitted to occur freely, no load or stress will be induced in the structure. In some cases where temperature deformation is not permitted, internal stress is created. The internal stress created is termed thermal stress.
Case 1- when the beam is fixed at both ends
For a homogeneous rod mounted between unyielding supports as shown, the thermal stress is computed as:

deformation due to temperature changes;
δT=αLΔT
deformation due to equivalent axial stress;
δP=PLAE=σLE
δT=δP
αLΔT=σLE
σ=EαΔT
where σ is the thermal stress in MPa, E is the modulus of elasticity of the rod in MPa.
Case 2- if the beam is partially fixed at both ends
If the wall yields a distance of x as shown, the following calculations will be made:
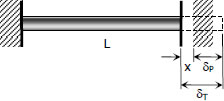
δT=x+δP
αLΔT=x+σLE
where σ represents the thermal stress.
Take note that as the temperature rises above the normal, the rod will be in compression, and if the temperature drops below the normal, the rod is in tension.
Case 3- if beam end free at one end
Case 3- if beam end free at one end
Due to change in temperature of material only strain is appear but no stress will appear.
Because we know that stress appears if two equal and opposite forces are acting on the body.








0 Comments
Thank for Visiting our site
we will Happy to see you here again